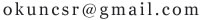已知a、b为正数，且（a/x)+(b/Y)=1，求证x+y大于等于（根号a+根号b)2

已知a,b为正整数,x,y>0且a\/x+b\/y=1,求证(x+y)≥(√a+√b)^2
已知a,b为正整数，x,y>0且a\/x+b\/y=1,则 (x+y）=（x+y)*(a\/x+b\/y)=a+b+ay\/x+bx\/y>=a+b+2根号（ab)=(√a+√b)^2

已知a,b,x,y属于R+且a\/x+b\/y=1,求x+y大于等于(根号a+根号b)^2
手机提问的朋友在客户端右上角评价点【评价】，然后就可以选择【满意，问题已经完美解决】了

a,b,x,y∈R正,a\/x+b\/y=1,求证x+y≥(√a+√b)^2
解1：柯西不等式 x+y=1*(x+y)=(a\/x+b\/y)(x+y)≥(√a+√b)^2 最后一步是柯西不等式。解2：基本不等式 x+y=(x+y)(a\/x+b\/y)=a+b+bx\/y+ay\/x >=a+b+2√ab =(√a+√b)^2

已知a,b为正实数,且(a\/x)+(b\/y)=1,求x+y的最小值?
∵(a\/x)+(b\/y)=1，x>0,y>0 ∴x+y=(x+y)(a\/x+b\/y)=a+b+ay\/x+bx\/y ∵ ay\/x+bx\/y ≥2√(ay\/x*bx\/y)=2√ab (当ay\/x=bx\/y时，取等号）∴a+b+ay\/x+bx\/y≥a+b+2√(ab)=(√a+√b)²∴x+y的最小值是（√a+√b)²...

已知啊a,b,x,y属于R+ ,a\/x+ b\/ y=1,求证x+y≥(根号a+根号b)²
左边=x+y =(x+y)*1 =(x+y)*(a\/x+b\/y)=a+b+ay\/x+bx\/y（由于ay\/x+bx\/y>=2√(ay\/x*bx\/y)=2√(ab)）>=a+b+2√(ab)=(√a+√b)^2 =右边 因此，不等式得证

已知a,b为正实数,且(a\/x)+(y\/b)=1,求x+y的最小值?
=（x+y）（1\/x+1\/y）=1+1+y\/x+x\/y ≥2+2√y\/x*x\/y =4 故,x+y的最小值为4 2（x+y）=（x+y）×1 =（x+y）（a\/x+b\/y）=a+b+ay\/x+bx\/y =5+ay\/x+bx\/y ≥5+2√（ay\/x）*（bx\/y）=5+2√ab =9 即2√ab=4 即ab=4 又由a+b=5 解得a=1，b=4或a...

若a\/x+b\/y=1且a,b,x,y∈( 0,+∞),求证x+y≥(√a+√b)∧2
(x＋y)=(x＋y)×[(a\/x)＋(b\/y)]=a＋b＋[(ay\/x)＋(bx\/y)]≥a＋b＋2√[(ay\/x)×(bx\/y)]=a＋b＋2√(ab)=(√a＋√b)²即：x＋y≥(√a＋√b)²

...b为正常数a+b=10,又x、y为正数,且(a\/x)+(b\/y)=1,若x+y的最小值为...
「Z-(A+B)」2≥4AB，因为X Y 是正变数 A B 是正常数，所以Z-(A+B)≥2√AB，即 Z=X+Y≥2√AB+(A+B）故X+Y的最小值是2√AB+(A+B）解法2：因为,A\/X+B\/Y=1所以X+Y=（X+Y)×(A\/X+B\/Y)=A+B+BX\/Y+AY\/X≥A+B+2√BX\/Y×AY\/X=A+B+2√AB（因为X Y 是正...

3已知a,b都是正数,x,y属于R,且a+b=1求证,ax平方+by平方大于等于(ax+b...
解： ax^2+by^2 - (ax+by)^2 = ax^2+by^2 - (a^2x^2+b^2y^2+2abxy)= ax^2 - a^2x^2 + by^2 - b^2y^2 -2abxy = a(1-a)x^2 + b(1-b)y^2 -2abxy 【此时利用条件a+b=1】= abx^2 + bay^2 - 2abxy = ab(x^2 + y^2 - 2xy)= ...

a,b为正数,a≠b,x,y∈(0,+∞),求证a2\/x+b2\/y>=(a+b)2\/x+y
我考虑的是这样的：关于第一问是Cauchy不等式的一种极特殊情况，只要将不等式写成(a^2\/x+b^2\/y)(x+y)≥(a+b)^2，再用Cauchy不等式即可，“=”成立的条件为a\/x=b\/y，关于第二问将f(x）写成f(x）=1\/x+1\/x+9\/(1-2x)，再利用上面的结论：f(x）≥(1+1+3)^2=25，当x=1\/5...