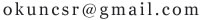得q=2或 q=1/2 (Q为公比) a1=1 或 a1=--16
则a3=4 或 a3=--4
已知等差数列{an}是递减数列,Sn为其前n项和,且S7=S8则最大值怎么求...
首先,由题意可知,{an} 是一个递减数列,这意味着它的通项 an 满足 an > an+1,对于所有的 n。另外,已知 S7 = S8,也就是前七项的和等于前八项的和。我们可以利用等差数列的和公式来求解这个问题。等差数列的前n项和 Sn 可以表示为:Sn = (n\/2) * [2a1 + (n - 1)d]其中,a1 ...
关于数列的题
1、由1\/2·A1+1\/2^2·A2+1\/2^3·A3+……+1\/2^n·An=2n+1,则1\/2·A1+1\/2^2·A2+1\/2^3·A3+……+1\/2^n-1·An-1=2n-1 将两者相减可得1\/2^n·An=2 所以·An=2^(n+1)2、对f(β)求导可得 f '(β)=2b^2sinβ\/(cosβ)^3 - 2a^2cosβ\/(sinβ)^3 ,令f...
一个数列题,望高手解答,谢谢
x1=1\/2,x2=2\/3,x3=3\/5,x4=5\/8,x5=8\/13 X6=13\/21 1) 数列Xn=an\/bn a1=1,a2=2,an=an-1+an-2 (n>=3)an=(1\/√5)[[(1+√5)\/2]^(n+1) - [(1-√5)\/2]^(n+1)]bn=an+1 Xn=[[(1+√5)\/2]^(n+1) - [(1-√5)\/2]^(n+1)]\/[[(1+√5)\/2]^(n...
关于数列的题
7.C 【解析】这是一道平方型数列的变式,其规律是8,9,10,11的平方后再加2,故括号内的数字应为12的平方再加2,得146。这种在平方数列基础上加减乘除一个常数的数列,初看起来显得理不出头绪,不知从哪里下手,但只要把握住平方规律,问题就可以化繁为简了。8.C 【解析】相邻两项相乘,可得1...
已知某等差数列第5项为14.第10项为29.求这个数列的前20项的和是多少...
某等差数列第五项是14,第十项是29,求该数列前20项之和。解析:这是一道关于等差数列求和题,题目告知了第五项和第十项值,可以据此求出数列的首项和公差,再根据前n项求和公式求出前20项和。解答:设数列首项是a,公差是d,根据题意得到方程组如下:a5=a+4d=14① a10=a+9d=29② ②-①得...
数列的有关题目
1、s17=17(a1+a17)\/2=17a9,与a8无关,所以不是一个确 定的常数。2、s15=15(a1+a15)\/2=15a8,所以是一个确定的常数。3、s8=8(a1+a8)\/2 因为只有a8确定,所以不是一个确定的常数。4、s7=7(a1+a7)\/2,与a8无关,所以不确定。所以确定的只有s15 了。二、解:因为 {an}是等比数列,...
8,23,54,(),188。这道题括号里该填多少?
这道题是一道数列题,能够按照已知的数列来肯定括号里应当填甚么数。察看问题中给出的数列,咱们能够发明这是一个等差数列,公役为 $23 - 8 = 15$。因而,括号里应当填一个等差数列中的下一个数,即 $54 + 15 = 69$。以是,谜底是 $8, 23, 54, 69, 188$。
关于数列的一道题
S3=a1+a2+a3=3a2 所以1\/3*S3=a2 S4=a1+a2+a3+a4=2(a2+a3)1\/4S4=(a2+a3)\/2 S5=a1+a2+a3+a4+a5=5a3 1\/5S5=a3 1\/3S3和1\/4S4等差中项为1 所以(a2+a3)\/2+a2=1 3a2+a3=2 由等比中项 a3²=a2*(a2+a3)\/2 2a3-a2a3-a2²=0 (2a3+a2)(a3-a2)=0 a3...
求一道高一简单的数列问题,谢谢
解:(1)设等比数列{an}的公比为q 又∵b1-a1=1,b2-a2=2,b3-a3=3,且{bn}是等比数列 ∴(2+q)²=2(3+q²)∴q=2±√2 ∴an=(2+√2)²或an=(2-√2)²(2)由(1)知:(2+aq)²=(1+a)(3+aq²)整理得:aq²-4aq+...
一道等比数列数学题求解 在等比数列{an}中,已知S3=4,S6=36,求an_百度...
S3=a1(1-q^3)\/(1-q)=4 a1\/(1-q)=4\/(1-q^3) ……… ① S6=a1(1-q^6)\/(1-q)=36 a1\/(1-q)=36\/(1-q^6)a1\/(1-q)=4\/(1-q^3)=36\/(1-q^6)1\/(1-q^3)=9\/(1-q^3)(1+q^3)整理得到q^3=8 q=2 将q=2代入① 可以得到a1=4\/7 所以根据公式得到 an=a1...