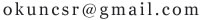再算定积分=8-1-0-[16-4-8ln2]=8ln2-5
你看下你积分哪里算错了
定积分,一个疑问。
“把t+a看成一个整体,∫ f(t+a)d(t+a) =∫f(x) dx 这样直接代换掉”,不可。那相当于作替换x=t+a,则积分限也要随之替换,则未能证出。方法二,[a,a+T]=[a,0]+[0,T]+[T,a+T]在[T,a+T]上作替换。
定积分的一个疑惑
你只需记住一点,只有你把积分变量换了,才需要改上下限,如果积分变量没换,只是凑微分时d后面的东西发生变化,一律不需要改上下限。或者也以理解为:第一类换元不需要改上下限,第二类换元才要改上下限。因此:1、dt=d(t+C)不需要改上下限;2、dt=(1\/2)d(2t)也不需要改上下限;道理很简单,...
利用定积分定义求数列和的极限疑问,急急急!
所以,我们必须考虑在闭区间内,定积分是否存在。而定积分包括暇积分,对 于暇积分,是必须计算极限的的,极限不存在就是积分不收敛。两者是一致的。2、只要有闭区间存在,那都可以进行n等分。答:错了。请参见上面的解释。3、这不是循环逻辑么?答:这不是循环逻辑。这里只是说,被积函数在给定的...
高等数学中,关于定积分的基本性质疑问,谢谢!
1、∫f(t)dt,是关于t的积分,,即把f(t)中的所有含t的项积分 由于x不随t的变化而变化。此处x是特定的常数,∫xf(t)dt=x∫f(t)dt。2、f(x)是x的函数,与t的变化无关,不随t的变化而变化,则成立。
关于定积分性质的一个疑问
当然是成立的。你的第一个例子中,当a>b时,从a到b的关于f(x)的定积分=负的从b到a的关于f(x)的定积分。那么同样b
定积分中对dx的一点疑问!
x=t^2,那么dx=d(t^2)=2tdt 其实就是dx\/dt=x'(t)=2t 这样就好理解了
关于定积分的一个疑问 ∫1\/((x^2)+(a^2))^(1\/2) dx(a>0) 书中令x=at...
1、“辅助三角形的任何一个角的范围是在0度到180度之间”.这种概念是初学者,或者说,是初中生的概念,不能推广到积分的变量代换.学到三角函数、解析几何就知道,角度可以为负,表示的是方向问题.具体体现就是象限的问题.负角的概念并不是真的有个角是比0还要小的负值.仅仅是旋转的方向问题.2、arctan...
高数定积分的疑问
它是令t=-x,改变了积分变量,将x用-t代换之后,原来x的积分区域是(-a,0),对应的t的积分区域就变成-x的范围,也就是变成了(a,0)
定积分定义 的疑问
无穷多个高阶无穷小加起来当然不等于0,而是等于你要求的这个面积,这也就是积分的目的。积分就是把X轴分成多段,每段长都是dx,因此相邻的两个曲边梯形,他们在X轴上的位置就是差一个dx。当分段达到无穷多,dx的长度也就是无穷小了,但是由于乘出来的面积不是0,所以这是一个高阶无穷小。
关于定积分的一点疑问
第一个概念错误:面积为正当然不错,但是必须是上方的函数f(x)减下方的函数g(x)才行,积分的结果才是正。本题x在x²上方,只有[0, 1]这一段。所以a,b不可以任意定。第二个概念错误:本题只有在[0,1]内的积分才是正值。在此区间外的积分都是负值。要想得到最大值(指正值,不是指...