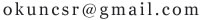把腰长为1的等腰三角形折叠两次后,得到的一个小三角形的周长是
把腰长为1的等腰三角形折叠两次后,得到的一个小三角形的周长是
A.1+根号2 B.1+2分之根号2 C.2-根号2 D.根号2-1
...三角形折叠两次后,得到的一个小三角形的周长是__
根据勾股定理可知腰长为1，则斜边为 2 ，折叠后所得的三角形与原三角形相似，但斜边成了1，所以相似比是 2 ：1 ，同理第三个小三角形与第二个三角形的相似比也 2 ：1 ，得到第三个三角形的斜边是 2 2 ，所以第一个与第三个的相似比是 2 ： 2 ...
...把腰长为1的等腰直角三角形折叠两次后,得到的一个三角形的周长是...
最后三角形的直角边=1\/2,所以得到的三角形周长=(1\/2)x2+根号2\/2=1+根号2\/2
求小等腰直角三角形的周长
想象一下可知，折两次真好是到相同位置，边长变为原来一半~所以折叠四次后，边长变为原等腰直角三角形的(1\/2)*(1\/2)=1\/4 即，小等腰直角三角形的周长是原等腰直角三角形周长的1\/4 选择B
把一张长方形纸照下面的方法对折两次再打开
一张长方形纸对折两次得出的图形有三个答案哦。1、把一张长方形连续横向折叠两次，可以折出小长方形。2、把一张小长方形先横向对折再竖向对折，可以折出小正方形。3、把一张长方形沿对角线对折，再对折一次，可以折出三角形。所以把一张长方形对折两次，可以得出小长方形，小正方形，三角形。长方形...
一张长方形纸对折两次后展开折痕
继续折叠纸，每次折叠都会在新的方向上产生一条新的折痕，每一条折痕的方向都与上一条垂直。因此，折叠两次后，我们总共会得到四条折痕，它们分布在纸的不同方向上。所以，折叠两次后，总共会得到4条折痕，它们分别是：1、长度方向上的折痕。2、宽度方向上的折痕（与第一条垂直）。3、长度方向上的...
一个等腰三角形按对称轴折叠4次,新的三角形周长是旧的几分之几?
折叠四次则面积是旧的16分之1，那么周长就是旧的4分之一。你说的三角形应该是等腰直角三角形吧，，不然没法对折4次，这样是不是直接能算出来了呢？而且能很快算出来。还有你补充的为什么，是这样的：折叠一次面积是原来的一半，两次则是一半的一半，即1\/4，三次则1\/8，四次则是1\/16，n次则是...
长方形对折两次折痕的关系是
当长方形沿对角线折叠时，形成的两条折痕分别是相互垂直的。这是对角线将长方形分成两个等腰直角三角形，每个三角形的两条边正好是折痕。根据几何原理，等腰直角三角形的两条直角边与斜边是相互垂直的。长方形对折两次所形成的折痕之间呈垂直关系。这种关系保持了长方形的形状完整性，还展示了几何学中的...
一个正方行折叠两次后一个小长方形的周长是40米,问元来的正方形周长是...
解:设折叠前正方形的边长为L则折叠后小长方形的周长为2L+2X1\/4L=40∴L二16∴原耒的正方形周长为4L二64米
把一张圆形纸片对折两次后,形成的折痕会是什么图形?
把一张圆形纸片对折两次后，形成的折痕将形成一个等边三角形、一个菱形、一个五角形和一个八角形，这些形状的边长都等于圆的半径。1、这些折痕将形成一个等边三角形。这是因为每次对折都会将圆分成两等分，而三角形的每个角都是60度，因此折痕之间的角度将是60度。2、这些折痕将形成一个菱形。这个菱形...
圆形的折纸方法
2、将上面形成的等腰三角形沿着高对折。这意味着将三角形的顶部和底部的两个角向内折叠，使其形成一个小于上一个三角形的形状。3、再将上面等腰三角形对折两次，每次都是将两个相对的边对齐，然后压平。这样会形成一个小小的长方形。然后用铅笔在长方形的边缘处画一条曲线。4、用剪刀沿着之前画好的...
