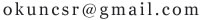则|x|=c,|y|=4/3
焦点到渐近线的距离为2,即b=2 (由tanA=b/a,sinA=b/c, 得2=csinA=b)
所以
c^2/a^2-(4/3)^2/b^2=1
(a^2+2^2)/a^2-(4/3)^2/2^2=1
a=3
2a=6
圆锥曲线2—双曲线基础知识
首先,双曲线定义为平面内两点(焦点)的距离之差的绝对值恒为常数的点集。其标准方程为:(x^2\/a^2)-(y^2\/b^2)=1或(y^2\/a^2)-(x^2\/b^2)=1,焦点位于x轴或y轴。双曲线的焦点间距离即为焦距,实轴的长度则为2a或2b。离心率e为双曲线的焦点到双曲线最近点距离与焦距之比,范围在(1...
圆锥曲线(2)双曲线
本文深入解析圆锥曲线中的双曲线概念,让我们从第一定义出发。上期内容回顾:椭圆的特征是到两个焦点的距离之和恒定,那么平面上到两个特定点(焦点)的距离差为定值的点的集合,即为双曲线!通过图形演示,这一猜想得到了验证。双曲线的第一定义是:在平面上,到两个固定点(焦点)的距离之差恒定。图...
圆锥曲线二级结论?
圆锥曲线常用的二级结论:1、椭圆∶焦半径∶a+ex(左焦点),a-ex(右焦点),x=a²\/c。2、双曲线∶焦半径∶|a+ex|(左焦点)|a-ex|(右焦点),准线x=a²\/c。3、抛物线(y²=2px)∶焦半径∶x+p\/2准线∶x=-p\/2。扩展知识 1.什么叫圆锥曲线 圆锥曲线,是由一平面截二次锥...
圆锥曲线第二定义
第二定义:到定点的距离与到定直线的距离之比为定值的所有点的集合是圆锥曲线。第三定义:顶点在原点,距离相等。
圆锥曲线的第二定义是什么意思?
圆锥曲线第二定义是:到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0<e<1时为椭圆:当e=1时为抛物线;当e>1时为双曲线。圆锥曲线包括椭圆(圆为椭圆的特例)、抛物线、双曲线。圆锥曲线特点:1、从方程的形式来看:做直角坐标系中,这几种曲线的方程(包括圆)f(x,y)=0...
【圆锥曲线】第二定义以及焦半径倾斜角式、坐标式及相关推论
一、焦半径倾斜角式 设圆锥曲线上点的坐标为(x,y),焦点为(Fx,Fy),焦半径与焦点所在轴正方向的夹角为α,焦半径为d,则焦半径与焦点的关系满足以下公式:d=|Fx-x|\/cos(α) + |Fy-y|\/sin(α)其中,α为焦半径方向与焦点所在轴正方向的夹角。二、推论 1.在椭圆和双曲线中,焦半径与焦点的...
圆锥曲线两交点长的公式
圆锥曲线两交点的长公式为:$$d=sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$其中,$(x_1,y_1)$和$(x_2,y_2)$是圆锥曲线上两个交点的坐标,$d$为两点之间的距离。
高中数学圆锥曲线公式总结
高中数学圆锥曲线公式总结 1.焦半径公式 ,P为椭圆上任意一点,则│PF1│= a + eXo │PF2│= a - eXo (F1 F2分别为其左,右焦点)2.通径长 = 2b2\/a 3.焦点三角形面积公式 S_PF1F2 = b2tan(θ\/2) (θ为∠F1PF2)(这个可能有点难理解,不过结合第一定义可以较快的推,双曲线的也是...
圆锥曲线第二定义
椭圆是一种圆锥曲线(也有人叫圆锥截线的),现在高中教材上有两种定义:1、平面上到两点距离之和为定值的点的集合(该定值大于两点间距离)(这两个定点也称为椭圆的焦点,焦点之间的距离叫做焦距);2、平面上到定点距离与到定直线间距离之比为常数的点的集合(定点不在定直线上,该常数为小于1的...
如何用几何画板画圆锥曲线的z^2
z^2=x^2+y^2的图像如下图所示:通过一个定点V且与定曲线r(它不过定点V)相交的所有直线构成的曲面称为锥面;如果母线是和旋转轴斜交的直线,那么形成的旋转面叫做圆锥面,这时,母线和轴的交点叫做圆锥面的顶点。